一起来学统计学（1）-- 描述性统计

2019-07-15 #统计学 #作业

前言

数据分析首先要学会描述众多繁杂数据的概况，针对结构化数据都可以分为三种描述方式：数据的集中趋势、数据的离散程度以及数据的分布形态，其中每种描述方式又分为若干详细的数据特征描述指标具体如下图：

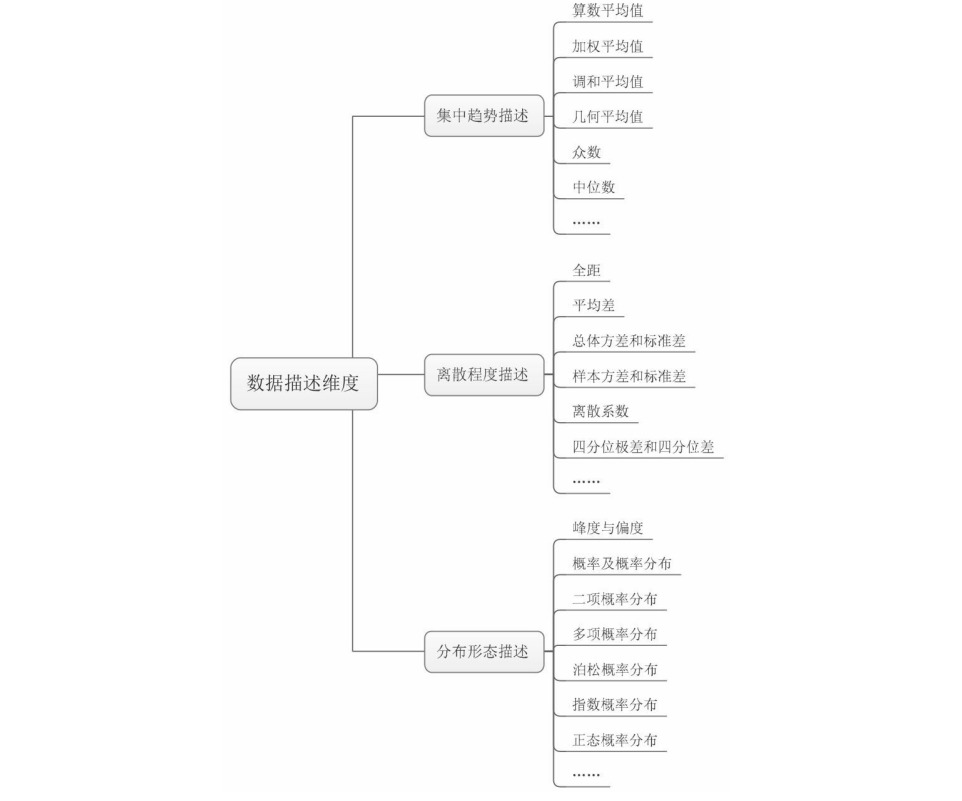
1563331838382

今天我们就来详细的说一下其中的几个重点指标，并且用python简单实现帮助理解。

数据集中趋势描述

算数平均数

比较简单，直接上代码

# 算数平均数
def avg(num_list):
    return sum(num_list)/len(num_list)

加权平均数

把数据按照权重分组，分别乘以各自的权重后相加除以权重之和

几何平均数

数据集每个相乘开根号count(1)，一般用户比例，增长百分比，增长数率等情况

# 几何平均数
def avg_geometry(num_list):
    sum = 1
    if num_list and len(num_list) > 0:
        length = len(num_list)
        for num in num_list:
            sum *= num
        return math.pow(sum, 1.0/length)

分位数

将一个随机变量的概率分布范文分为几个等分的数值点，常用有中位数，四分位数，百分位数。一般需要将数据排序，再取相应分为值，如分为值数据有两个不同的数值那么取这两个数据值的平均数。

# 中位数/分位数
def median(num_list, split_num=2):
    num_list.sort()
    length = len(num_list)
    result = []
    if not split_num or split_num == 2:
        if length % 2 == 0:
            return (num_list[int(length/2-1)] + num_list[int(length/2)])/2
        else:
            return num_list[length/2-1]
    else:
        if length % split_num == 0:
            i = split_num
            while i > 1:
                result.append((num_list[int(length / i - 1)] + num_list[int(length / i)]) / 2)
                i -= 1
            return result
        else:
            i = split_num
            while i > 1:
                result.append(num_list[int(length / i - 1)])
                i -= 1
            return result

众数

出现次数最多的那个数值

# 众数
def mode(num_list):
    dict = {}
    result = []
    max = 0
    if num_list and len(num_list) > 0:
        for num in num_list:
            if num in dict:
                dict[num] += 1
            else:
                dict[num] = 1
        d1 = sorted(dict.values(), reverse=True)
        max = d1[0]
        for num in dict:
            count = dict.get(num, 0)
            if count == max:
                result.append(num)
    return result

数据离散程度描述

极差

全部数据的距离又叫全距，最大最小值的差

平均差

又叫平均偏差，为了消除符号的影响使用绝对值的方式聚合每个值与平均数的差，再除以总个数

# 平均差
def average_deviation(num_list):
    avg_num = avg(num_list)
    return sum([abs(num-avg_num) for num in num_list])/len(num_list)

方差

使用平方的方式消除符号的影响，但是这样做会夸大离散程度

# 方差
def variance(num_list):
    avg_num = avg(num_list)
    return sum([math.pow(num - avg_num, 2) for num in num_list])/len(num_list)

标准差

方差的平方根，可以消除方差对于离散程度的夸大

# 标准差
def standard_deviation(num_list):
    return math.pow(variance(num_list), 1.0/2)

四分位差

四分位极差等于第一四分位数与第三四分位数的差值（Q3-Q1），这个差值区间包含了整个数据集合50%的数据值。

异众比率

分类数据描述，不是众数在总数占比

# 异众比率
def variation_ratio(num_list):
    count = 0
    mode_nums = mode(num_list)
    for num in num_list:
        if num not in mode_nums:
            count += 1
    return count/len(num_list)

离散系数

对于相对离散程度的描述，又叫变异系数使用标准差/平均数得到。当对比两个集合方差和标准差相等时，可以使用离散系数进行对比离散程度。

# 离散系数 
def coefficient_dispersion(num_list):
    return standard_deviation(num_list)/avg(num_list)

离散程度这里其实还有更多可以深入研究的点，比如样本方差与自由度，刚兴趣的可以阅读下文（https://www.zhihu.com/question/20099757/answer/658048814）

数据分布形态

这里的数据分布主要指的是概率分布，概率分布是指事件的不同结果对应的发生概率所构成的分布，形态一般可以使用图形表示。这里先引出其中的两个指标，下一章节将会详细的说概率分布。

正态分布

正态分布式连续型概率分布的一种，它表明被测事物处在稳定的状态下，自然环境和人类社会的很多事物都会自发形成稳定的系统因此，在这些环境下，许多事物和现象的分布都服从正态分布。正态分布长这样：

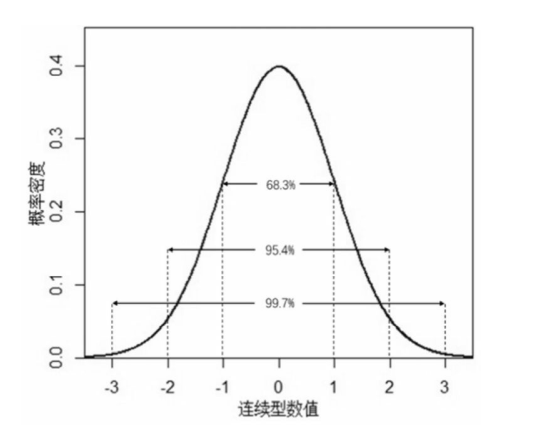
1563336461161

正态分布的形态主要取决于平均值与标准差，均值决定正态分布曲线在横轴上的位置，而方差则决定正态分布曲线是高耸还是平缓的程度。对于服从正态分布或近似服从正态分布的数据总体，它们的均值为μ，标准差为σ，经验法则可以表述为大约有 68.3%的数据会落在区间μ±σ内，大约95.4%的数据会落在区间μ±2σ内，大约99.7%的数据会落在区间μ±3σ内，所以经验法则也被形象地称为六西格玛（6σ）法则

偏态系数

又叫峰态系数，一般用于连续型的单峰分布的形态。因为只有一个波峰，当波峰偏离正态分布的波峰时就出现了偏态系数；即当偏态系数=0为正态分布，当偏态系数>0时为右偏态，当偏态系数<0时为左偏态。

计算时使用平均值与中位数之差除以标准差。

# 偏态系数
def skew_coefficient(num_list):
    return (avg(num_list)-median(num_list))/standard_deviation(num_list)